Rotacional, Divergencia , y Gradiente

Rotacional 

Se entiende por rotacional al operador vectorial que muestra la tendencia de un campo a inducir rotación alrededor de un punto. También se define como la circulación del vector sobre un camino cerrado del borde de un área con dirección normal a ella misma cuando el área tiende a cero (Ecuación 1).

(1)

Aquí, S es el área de la superficie apoyada en la curva C , que se reduce a un punto. El resultado de este límite no es el rotacional completo (que es un vector), sino solo su componente según la dirección normal a S y orientada según la regla de la mano derecha. Para obtener el rotacional completo deberán calcularse tres límites, considerando tres curvas situadas en planos perpendiculares.

El rotacional de un campo se puede calcular siempre y cuando este sea continuo y diferenciable en todos sus puntos.

El resultado del rotacional es otro campo vectorial que viene dado por el determinante de la siguiente ecuación:

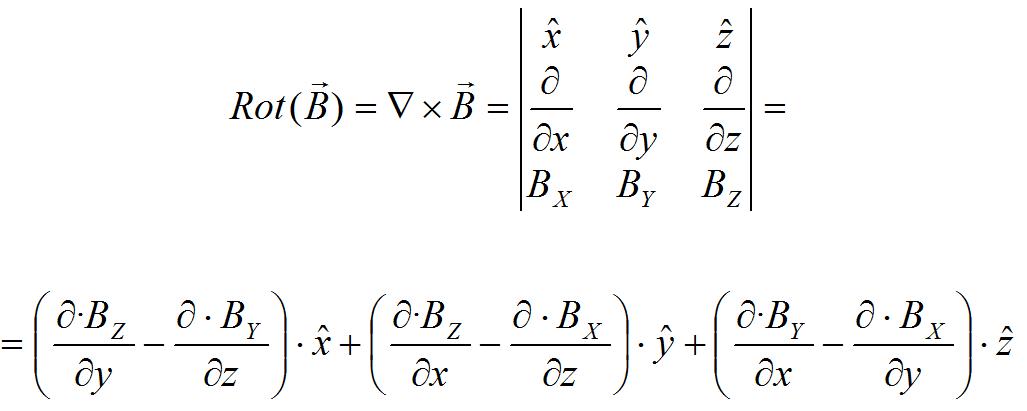(2)

Las propiedades más destacadas del rotacional de un campo son:

•  Si el campo escalar f(x,y,z) tiene derivadas parciales continuas de segundo orden entonces el rot (f) =0

•  Si F(x,y,z) es un campo vectorial conservativo entonces rot (F) = 0

•  Si el campo vectorial F(x,y,z) es una función definida sobre todo  cuyas componentes tienen derivadas parciales continuas y el rot (F) = 0, entonces F es un campo vectorial conservativo.

Divergencia

La divergencia de un campo vectorial mide la diferencia entre el flujo entrante y el flujo saliente en una superficie que encierra un elemento de volumen dV . Si el volumen elegido solamente contiene fuentes o sumideros de un campo, entonces su divergencia es siempre distinta de cero.

La divergencia de un campo vectorial en un punto es un campo escalar, que se define como el flujo del campo vectorial por unidad de volumen conforme el volumen alrededor del punto tiende a cero, para el caso del campo magnético la divergencia viene dada por la ecuación

(3)

donde S es una superficie cerrada que se reduce a un punto en el límite, B es el campo magnético, V es el volumen que encierra dicha superficie S y es el operador nabla, que se clacula de la sigueinte forma:

(4)

La divergencia de un campo es un valor escalar con signo. Si este signo es positivo, quiere decir que el campo emana hacia el exterior de dicho punto y, por tanto, es una fuente o manantial. Si el signo es negativo, el campo converge hacia un punto del interior del volumen, por lo que constituiría un sumidero. Si la divergencia fuese cero el campo neto (diferencia entre las líneas entrantes y salientes) sería nulo.

Gradiente

En análisis matemático (cálculo avanzado), particularmente en análisis vectorial, el gradiente o también conocido como vector gradiente,​ denotado  de un campo escalar es un campo vectorial. El vector gradiente de  evaluado en un punto genérico  del dominio de , (), indica la dirección en la cual el campo  varía más rápidamente y su módulo representa el ritmo de variación de  en la dirección de dicho vector gradiente. 

El gradiente se representa con el operador diferencial nabla  seguido de la función (atención a no confundir el gradiente con la divergencia, esta última se denota con un punto de producto escalar entre el operador nabla y el campo). También puede representarse mediante , o usando la notación . La generalización del concepto de gradiente a campos  vectoriales es el concepto de matriz Jacobiana.​